How to Tell if Vector Spans R3

You need three vectors to span R3 you have two so the answer is no. A set of vectors from R³ will span R³ if it is a basis set that is to say that it should be a linearly independent set such that each every element x R³ can be written as a linear combination of the elements from this set.

Determine If The Unit Sphere Is A Subspace Of The Vector Space R 3 Maths Exam Math Videos Algebra

If v xyz reduce the augmented matrix to 2 4 1 2 4 x 0 1 1 x y 0 0 0 7x11y z 3 5.

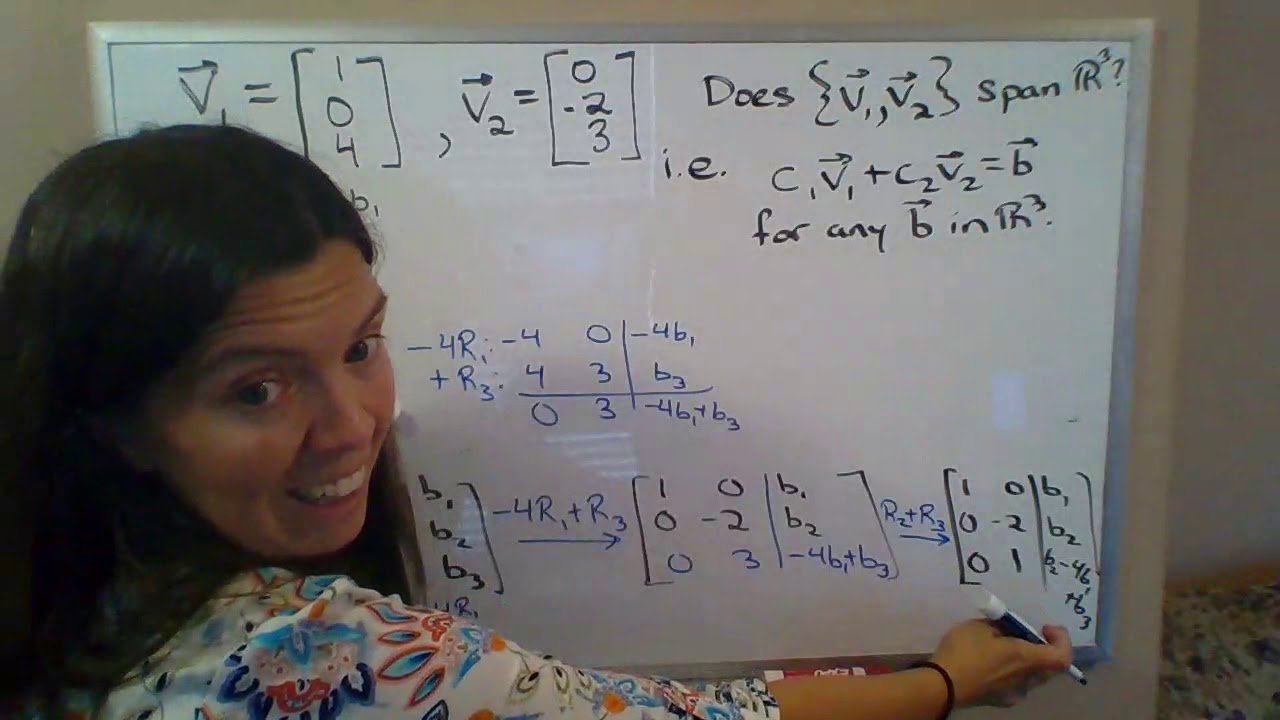
. Put the three vectors into columns of a 3x3 matrix then reduce. Recall that any three linearly independent vectors form a basis of R3. Its a years since I took Linear Algebra so I give no guaranties.

If r3 and the vectors are in R3 then this must be the whole space. Support Author Jonathan David. I could have c1 times the first vector 1 minus 1 2 plus some other arbitrary constant c2 some scalar times the second vector 2 1 2 plus some third scaling vector times the third vector minus 1 0 2.

So let me give you a linear combination of these vectors. Spanv₁ v₂ v₃ R². Learn the definition of Span x 1 x 2 x k and how to draw pictures of spans.

One may also ask can two vectors span r3. For example you could look at the null space and use the rank-nullity theorem. Put the vectors in a matrix row reduce and the number of pivots you get is the dimension of the span of the vectorsFirst video introducing spans.

This has a solution only when 7x11y z 0. You can determine if the 3 vectors provided are linearly independent by calculating the determinant as stated in your question. Also a spanning set consisting of three vectors of R3 is a basis.

For an arbitrary v 2R3. Then the span of v 1 and v 2 is the set of all vectors of the form sv 1 tv 2 for some scalars s and t. An inconsistent system of equations a consistent system of equations spans in R 2 and R 3.

If you get the identity not only does it span but they are linearly independent and thus form a basis in R3. The span of a set of vectors is the set of all linear combinations of the vectorsFor example if and. In R3 it is a plane through the origin.

Span 1 3 2 6 is 1-dimensional as 1 3 12 x 2 6 Span 1 0 0 0 1 0 1 1 0 is 2-dimensional as 1 0 0 0 1 0 1 1 0 To predict the dimensionality of the span of some vectors compute the rank of the set of vectors. The span of three vectors in R3 that do not lie in the same plane is all of R3. Please support my work on Patreon.

The span of a single vector is all scalar multiples of that vector. Two vectors cannot span R3. To span R 3 you need 3 linearly independent vectors.

Spanv₁ v₂ R² if theyre not collinear. Solve a vector equation using augmented matrices decide if a vector is in a span. R 3 3 vectors they will span R 3 if and only if they are linearly independent -- for this reason it suffices to check determinants.

However thats not the only way to do it. Thus the span of these three vectors is a plane. If you have exactly dim.

We prove that the set of three linearly independent vectors in R3 is a basis. R 3 3 vectors. If your last row is only zeros then the set does not span R3.

Three Vectors Spanning R3 Form a Basis for the proof of this fact a Sleft beginbmatrix 1. They do not span R3. Considering this what is the span of a vector.

Option i is out since we cant span R 3 with less than dim. Part 2 of example. Three vector or more.

Answer 1 of 3. The columns - or rows - of a rank r matrix will span an r-dimensional space. See the post Three Linearly Independent Vectors in R3 Form a Basis.

If you have 3 linearly independent vectors that are each elements of R 3 the vectors span R 3. So a set of 3 elements of R³ can span R³ iff it is. To your second question if you have three vectors and rref the set spans R3 if you have three pivots.

Our aim is to solve the linear system Ax v where A 2 4 1 2 4 1 1 3 4 3 5 3 5and x 2 4 c 1 c 2 c 3 3 5. To span R3 that means some linear combination of these three vectors should be able to construct any vector in R3. B 110 012 and 131.

Other than two vectors are all REDUNDANT. The span of a set of two non-parallel vectors in R2 is all of R2. In R2 or R3 the span of a single vector is a line through the origin.

Does A Set Of Vectors Span R N Youtube

Determine Whether Vectors Span R3 And Is The Collection A Basis Youtube

Determine Whether A Collection Of Vectors In R 3 Spans R 3 Youtube